先日、DynamoDB設計の背景にあった可用性とスケーラビリティの両立に対するAmazonのアツい想いについて書いた:
背景だけだと寂しいので、ここではもう少し詳しく、DynamoDBの実装を支える Replication と Partitioning の基本、そして Consistent Hashing について、"Designing Data-Intensive Applications" (DDIA) の解説も踏まえてまとめておく。
Replication
DynamoDB(分散DB)が考えるべき問題の1つに、データのコピーをネットワーク上の複数のマシン(ノード)で保持する Replication(レプリケーション)がある。
データのレプリカを作成する目的はいくつかあって、DDIAのまとめを引用すると:
- High availability
- あるマシンが死んでもシステムを動かし続ける
- Disconnected operation
- 1つのマシンのネットワークが途絶えてもアプリケーションは動き続ける
- Latency
- データをレプリカという形で地理的により近いところにおけば、ユーザはそのデータにより早くアクセスできる
- Scalability
- 複数のレプリカに対してreadを実行することで、一台のときよりも多くのreadがさばける
などが挙げられる。
そして、レプリケーションを実現する際の難しさは『いかにレプリカの変更を扱うか(同期するか)』という一点に集約されていると言っても過言ではない。
複数のノードがあったとき、データの書き込みリクエストを特定のノード(リーダ; master)に集約して、リーダからその他のノードたち(フォロワー;slave)へ変更を通知する―これが Leader-based replication と呼ばれる考え方だ。
対して、DynamoDBは特別な役割を担うノードを持たず、書き込み先やその順序について何ら制約を与えない Leaderless replication という方針をとった。DDIAによると、Leaderless replication は一度は廃れた手法だったものの、DynamoDBが採用したことで再び脚光を浴びたという。今ではRiak, Cassandra, Voldemortなど、多数のDynamoチルドレンが存在する。
Quorum reads and writes
『データの変更をレプリカ間で適切に同期する』ということがどれだけ難しいかは、Leaderless replication では複数レプリカに対して並列にread/writeリクエストが投げられることを考えれば明らかだろう。たとえば、ある一台のレプリカへの読み込み/書き込みが失敗した場合はどうすればいいのか。そもそも、システムは何をもって「今読んだデータが確かに最新のものだ」と判断するのか。
この点についてDynamoDB論文では、一般に "Quorum reads and writes" と呼ばれる考え方の下でシステムの動作保証を議論している1。
いま、レプリカが n 台あって、read時には並列に r 台のノードに問い合わせを行い、write時は最低 w 台のノードに対して書き込みが完了して初めて『成功』とみなされるシステムを考える。
ここで Quorum reads & writes を考えると、システムは w + r > n を満たす限り、readリクエスト時に最新のデータがいずれかのレプリカから得られることを“保証”する。
この不等式は移項するとイメージしやすいと思う。w + r > n とは r > n - w であり、w はシステムが書き込み操作を『成功』と判断する最低ラインだった。つまり、システムへの書き込み操作が『成功』したのなら、最低でも w 台のレプリカは確実に最新のデータを持っている。逆に言えば、n - w 台のレプリカに関しては、何らかの理由で最新のデータが書き込まれていない可能性があり、n - w = # of potentially legacy nodes といえる。
すなわち r > n - w とは、想定しうる『データが最新ではないノード』の最大数 n - w よりも多くのノードに毎回readリクエストを投げれば、少なくとも1台のレプリカからは最新のデータが得られるハズ、という話。
この考え方のポイントは、ユーザがパラメータ n, w, r を自由に調整できる点にある。『AmazonのDynamoDB論文を眺めた』でも書いたとおりAmazonはSLAを超重視するので、サービスに応じてトレードオフが調整可能であることはとても重要だった。
たとえばwriteよりもreadが圧倒的に多いサービスの場合、究極的には w = n, r = 1 とすると、readは1台だけ読めばいいので高速になる。しかしその分、書き込みの際は全ノードに確実に最新のデータを書き込まねばならず、これは並列分散環境下では最高に厳しい条件といえる。
なお、DDIAによると、n は 3, 5 あたりの奇数、w = r = (n+1)/2(=半分より多い)くらいに設定されることが多いらしい。なぜなら、w = r = (n+1)/2 なら、最大で n/2 台まではノードが死んでいても書き込み、読み込みが成功するから。これが "Quorum" という概念が“多数決”に例えられるゆえんかな。
ちなみに、Dynamo論文ではノード単位の一時的な障害によってread/writeがコケないように Hinted Handoff というアイディアも取り入れている。
これは、あるノードに対するread/writeが失敗した際、データを「本来どのノード(レプリカ)が受け取るべきだったか」という情報(ヒント)付きで別ノードのローカルストレージに一旦保存しておくというもの。そしてシステムはこれを定期的に監視して、本来受け取るべきだったひとが復旧したところで、ヒント付きのオブジェクトの再送、破棄を行う。
つまり、Hinted Handoffを実装することで、一時的な障害、ダウンによって生じるread/writeの損失が防げる。
ヒント付きオブジェクトの存在も踏まえて Quorum を議論するのが Sloppy Quorum というものだ。これは相変わらず r + w > n という要件は必須で、最低でも w, r 台のノードから成功レスポンスを受け取る必要があるが、ローカルストレージに一時保存しているread/writeリクエストも『成功』としてカウントする、ゆるい制約。
Versioning
DynamoDBは Eventual Consistency 2 なスタンスなので、レプリカの更新は非同期に行われる。そのためQuorumだけでデータの“正しさ”を完全に保証することは難しく、readで古いデータが返ってくる可能性は未だ排除しきれない3。
しかし、たとえある時点では最新でなくとも、ユーザが実行した処理の結果はいずれ (eventual) 確実に反映したい。そこで、オブジェクトの Versioning(バージョニング)によって各変更をimmutableな形で保持して、順次反映していく戦略をとる。
たとえば、ひとつのオブジェクトが複数のバージョンを持っていてコンフリクトが発生した場合、両者をマージすることでゆるゆると一貫性を担保する方向へ進んでいくことになる。
Partitioning
レプリケーションと並んで議論されるテクニックに、膨大なデータを複数ディスクに分散させる Partitioning(パーティショニング)がある。これにより、ロードを各ノードのプロセッサで分散してさばくことができるので、スケーラビリティ向上が期待できる。
もっと言えば、通常はパーティショニングを行い、各パーティションについてレプリカをつくる、という組み合わせ的アプローチがとられる。
パーティショニングの難しさは『いかにロードが偏り無く分散するようにパーティションを切るか』という点にある。たとえデータを分散させても、ある特定のディスク上のデータにアクセスが集中すると、そこがホットスポットとなってスケーラビリティ的に嬉しくない。
考えうる最もナイーブな分割方法のひとつとしてDDIAで挙げられているのは、キーが取りうる値をソートして並べて、それを分割して各パーティションに割り当てる方法。
たとえばタイムスタンプをキーに、各時刻でのデータ(値)を複数ディスクに保存するとき、『1日単位』でパーティションを切れば:
| Partition 1 | Partition 2 | Partition 3 | ... |
|---|---|---|---|
| 2017/12/01 00:00:00 - 23:59:59 |
2017/12/02 00:00:00 - 23:59:59 |
2017/12/03 00:00:00 - 23:59:59 |
... |
システムは各パーティションに属するキーの境界値、すなわち yyyy年MM月DD日 00:00:00 と 23:59:59 というタイムスタンプを覚えておけばよい。
ただし、この方法ではホットスポットを作りかねない。たとえば保存するデータがログのような現在時刻に対応して書き込まれるものなら、writeは確実に『今日』や『昨日』のパーティションに偏ってしまう。
このような状況を避けるべく、DynamoDB(分散DB)はキーのハッシュ値によってパーティションを決定する。“良い”ハッシュ関数を使えば、たとえ生のキーの出現パターンが偏っていても、それらを一様にパーティションに分配してくれるはず。
あるハッシュ関数 $h$ を使ってキーを $n$ 個のパーティションに分散させるなら、単純には $h(\textrm{key})\mod{n}$ に基づいてパーティションを割り当てればよさそうだ:
| Partition 1 | Partition 2 | Partition 3 | ... | Partition $n$ |
|---|---|---|---|---|
| $\mod{n} = 0$ | $\mod{n} = 1$ | $\mod{n} = 2$ | ... | $\mod{n} = n - 1$ |
しかし実際にはこれでは困る。
分散システムにおいて、スループットを上げるためにCPUを増やしたり、データサイズが増えたのでディスクを増やしたり、マシンが死んだので他のマシンが仕事を肩代わりするといったことは日常茶飯事で、パーティションの構成、すなわち $n$ の値はその都度変わりうる。
このような変化に対して、システムは適応的にデータの保存場所やリクエストを向ける先を変えていく必要があるが、$n$ が $n + 1$ になっただけでパーティションの配置 $h(\textrm{key})\mod{}$ はすべて1ずつズレることになり、その都度全データを再配置する必要が生じてしまう。
なので、剰余を使わずハッシュ値そのものでパーティションを切ったほうが、$n$ が増減したときに再配置されるデータが少なくなる。たとえば $h(\textrm{key}) \in [1, m]$ なら、$n$ 個のパーティションそれぞれの上界 $b_{n_i} = \frac{m}{n} n_i$ について:
| Partition 1 | Partition 2 | Partition 3 | ... | Partition $n$ |
|---|---|---|---|---|
| $h(\cdot) \in (0, b_1]$ | $h(\cdot) \in (b_1, b_2]$ | $h(\cdot) \in (b_2, b_3]$ | ... | $h(\cdot) \in (b_{n-1}, m]$ |
このように分割すればよい。
では具体的に、ノードの再配置はどのように行われるのか。ノード単位でのスケールアウト (incremental scalability) の実現を目標としていたDynamoDBにとって、効率的かつ効果的な再配置の手続き、すなわち、より良い動的なパーティショニング手法の実装は必須だった。
ここで登場するのが Consistent Hashing だ。
Consistent Hashing
Consistent Hashing は、もともとはCDNのようなネットワーク規模のキャッシュに対してロードを均等に分散させる一手段として提案された (cf. "Web Caching with Consistent Hashing")。
パーティショニングの文脈で、先の『ハッシュ値に応じてパーティションを均等に(いい感じに)割り当てる』というタスクにこれを応用する。
具体的には、ハッシュ関数の値域をあるリングで表現し、各ハッシュ値をリング内のブロックにマッピングしていく:
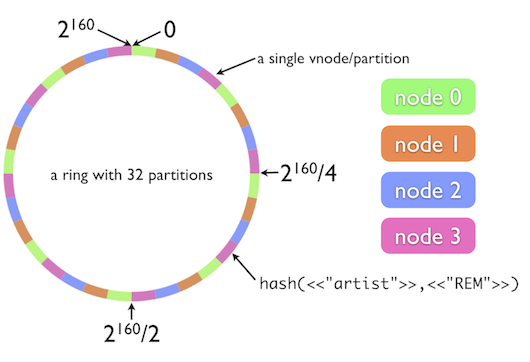
(図は "The Simple Magic of Consistent Hashing" より引用)
あるキーが与えられたとき、そのハッシュ値からリング内の場所を引く。そのキーに対応するデータは、その場所から時計回りに、次のキーの割り当て箇所までの間の数ブロック分に格納されるというワケ。
この挙動はコードを書いてみるとイメージしやすい (cf. "Consistent hashing | Michael Nielsen")。
まず、キーが与えられたときにリング内のある一点を返す関数 my_hash を実装する。先の表や図ではハッシュ値をそのまま使っているように見えたが、ここではMD5ハッシュの剰余を $[0, 1)$ の範囲内で正規化した値を用いる:
import hashlib
def my_hash(key):
"""Returns a hash value in a [0, 1) range.
"""
md5_hash_int = int(hashlib.md5(key.encode('ascii')).hexdigest(), 16)
n = 1000000
mod = md5_hash_int % n
return mod / float(n) # scale in a [0, 1) range
いま num_machines 台のマシンがあり、それぞれの num_replicas 台のレプリカをリング上に配置する場合、Consistent Hashing の挙動は次のようなコードで書き表せる:
import bisect
class ConsistentHash(object):
def __init__(self, num_machines=1, num_replicas=1):
self.num_machines = num_machines
self.num_replicas = num_replicas
# Allocate each replica (machine) onto a point of the unit circle
hash_tuples = [(mi, ri, my_hash('{}_{}'.format(mi, ri)))
for mi in range(self.num_machines)
for ri in range(self.num_replicas)]
# Sort replica assignment information based on its hash value
hash_tuples.sort(key=lambda t: t[2])
self.hash_tuples = hash_tuples
def get_machine(self, key):
h = my_hash(key)
# If a hash value is greater than the largest one (i.e., very close to
# 1.0 on the unit circle), cyclically back to 0.0.
if h > self.hash_tuples[-1][2]:
return self.hash_tuples[0][0]
hash_values = [t[2] for t in self.hash_tuples]
# Find the closest hash value and use corresponding machine (replica)
# to store a value of the key
index = bisect.bisect_left(hash_values, h)
return self.hash_tuples[index][0]
まず各マシン-レプリカのペアについて "[machine]-[replica]" という文字列をキーにハッシュ値を求め、(machine, replica, hash) のペアをハッシュ値順にソートして保持しておく。これがリング上での(時計回りに見たときの)ノードの割り当てに相当する。
そして、get_machine() は与えられた任意のキーのデータを保存すべきレプリカを見つけて返す。具体的には、与えられたキーのハッシュ値に最も近いハッシュ値を持つレプリカをリングから時計回りに探索して、その情報を返す(=ソート済み (machine, replica, hash) ペアの二分探索に相当)。
以上を利用すれば、7台のマシンについて、各3台のレプリカを用意した場合の Consistent Hashing は次のようにシミュレーション可能:
def main():
# Consistent Hashing over 7 machines and 3 replicas for each of them
ch = ConsistentHash(7, 3)
print('Allocation:\n(machine, replica, hash)')
for mi, ri, h in ch.hash_tuples:
print('({}, {}, {})'.format(mi, ri, h))
while True:
key = input('Enter a key: ')
print('Key `%s` is mapped onto a (scaled) hash value `%f`, and its value would be stored into a machine `%d`' % (key, my_hash(key), ch.get_machine(key)))
if __name__ == '__main__':
main()
課題だったノード(パーティション)の増減に関しては、隣接するキー(ハッシュ値)が担当する領域を拡大/縮小させるだけで対応でき。剰余で発生した『すべて再配置』よりもはるかに筋の良い手法だと言える。また、これならレプリカ間の境界値をその都度考えたり覚えたりする中心的な役割を担うノードも不要。
上の図ではリング状の一区画が "a single vnode/partition" と呼ばれているが、ここで言う vnode とは、Dynamo論文でも1つの“工夫”として導入されているバーチャルノードと呼ばれるアイディア。
オリジナルの Consistent Hashing は、ハッシュ値が(たまたま)偏ってしまうと特定のノードが担当する値域が極端に多く/少なくなってしまう。これはロードバランシング的に微妙だし、そもそも理想的にはノードごとのパフォーマンスの差異も考慮してパーティションを割り当てたい。
そこでDynamoでは、各ノードを円状の区画に一対一対応させず、追加のバーチャルノードというものを導入して、各ノードが円状の複数点に分散配置されるような仕組みを実装した。これについては『Virtual nodeについて』なども参照されたい。
レプリケーションで n, w, r がパラメータとして調整可能だったのと同様に、このバーチャルノードをいくつ用意するかはカスタマイズ可能であり、やはりこれもAmazonの思想、サービス形態的に嬉しいソリューションだと言える。
なおDDIAでは、このようなDBに対する Consistent Hashing の応用はそれほどうまく動かないことが既に知られており、(未だ話題になることは多いが)実際に使われることは稀だと言っている。そして、"Consistent" Hashing といわれると一貫性の話と混同しがちで紛らわしいので、単に Hash Partitioning と呼べば良いだろうに、とのこと。たしかに。
まとめ
AmazonのDynamo論文の実装パートに焦点をあてて、Replication, Versioning, Partitioning の概要と Consistent Hashing の挙動についてまとめた。
この手の話は概念的な部分と現実的な課題のギャップが掴みづらいので、論文だけだと腑に落ちない部分が多々あった。
そんな折、ちょうど "Designing Data-Intensive Applications" を読んで、この本が論文の行間を手厚く補ってくれたことに感動。結果としてつい長々と書いてしまったけど、乱暴に使いがちな『レプリカ』や『パーティション』という“当たり前”な用語・技術がなぜ大切か、なにが難しいか、という点をおさらいできたので満足です。
1. "Quorum" という概念はとても奥が深いらしい:『最近よく聞くQuorumは過半数(多数決)よりも一般的でパワフルな概念だった』 ↩
2. あわせて読みたい:『Eventual Consistencyまでの一貫性図解大全』 ↩
3. DDIAでは、より強い保証がほしければトランザクションやコンセンサスといった話題も組み合わせて考えてね、と言っている。 ↩
シェアする
カテゴリ
あわせて読みたい
- 2017-12-30
- "Designing Data-Intensive Applications"は濃密すぎる一冊だったので2018年の自分にも読んでもらいたい
- 2017-12-09
- AmazonのDynamoDB論文を眺めた
- 2017-04-09
- なぜSparkか
最終更新日: 2022-01-18
書いた人: Takuya Kitazawa(たくち)
長野県出身、カナダ・バンクーバーを拠点に活動するソフトウェアエンジニアです。10年以上にわたりB2B/B2Cの各領域でWeb技術・データサイエンス・機械学習のプロダクト化および顧客への導入支援・コンサルティングに携わってきました。現在は独立し、アフリカ・アジア・北米の企業や個人を対象に、テクノロジー戦略の策定・実装をお手伝いしています。アフリカのマラウイでは現地企業のICTディレクターとして、デジタル・トランスフォーメーションを推進中。詳しい経歴はCV を参照ください。いろいろなまちを走って、時に自然と戯れながら、その時間その場所の「日常」を生きています。ご意見・ご感想およびお仕事のご相談は [email protected] まで。
近況 一杯のコーヒーを贈る免責事項
- Amazonのアソシエイトとして、当サイトは amazon.co.jp 上の適格販売により収入を得ています。
- 当サイトおよび関連するメディア上での発言はすべて私個人の見解であり、所属する(あるいは過去に所属した)組織のいかなる見解を代表するものでもありません。
- 当サイトのコンテンツ・情報につきまして、可能な限り正確な情報を掲載するよう努めておりますが、個人ブログという性質上、誤情報や客観性を欠いた意見が入り込んでいることもございます。いかなる場合でも、当サイトおよびリンク先に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。
- その他、記事の内容や掲載画像などに問題がございましたら、直接メールでご連絡ください。確認の後、対応させていただきます。