昨年の話だけど、Courseraで開講されていた "Introduction to Recommender Systems" を履修・修了した。教えてくれたのはこの分野で知らぬ者はいない、ミネソタ大学のJoseph Konstan先生。2000年あたりの協調フィルタリングなど古典的な推薦手法に関する文献を漁ると、必ず彼のグループの論文にたどり着く。かの有名なMovieLensデータセット（画像処理でいうMNIST的な、定番データセット）も、このグループが提供している。
コースは全8回で内容は以下。
- Introduction to Recommender Systems
- 推薦システムの歴史やその背景
- Non-Personalized Recommenders
- 『最も人気のアイテムを常に推薦する』といった、個人化を行わない推薦手法
- Content-Based Recommenders
- TF-IDFに基づく推薦
- User-User Collaborative Filtering
- ピアソン相関係数およびコサイン類似度に基づく類似度計算と正規化の重要性
- ユーザ・アイテム間の行列における、ユーザ側の類似度に基づく推薦
- Evaluation
- 精度からセレンディピティまで、いろいろな評価指標
- Item Based
- ユーザ・アイテム間の行列における、アイテム側の類似度に基づく推薦
- ユーザベースとの比較
- Dimensionality Reduction
- 特異値分解、Matrix Factorizationによる行列補完
- Advanced Topics
- Cold-start問題など
※ 現在このコースはすでにCoursera上に存在せず、アップデート版の Recommender Systems Specialization が代わりに開講されている。しかし残念ながら有料なので、各トピックの詳細は上記目次を参考にしつつググってください :(
全体として、コンパクトに推薦システムの世界がまとまった非常に良い内容だった。この分野は新しい手法が次から次へと生まれておりトレンドを追うのも一苦労だが、どのような手法でも基本は変わらない。このコースの内容さえ理解していればとりあえず推薦システムは作れるし、その良し悪しを議論することもできるだろう。
各回には講義パートとインタビューパートがあり、インタビューパートではゲストを招いた対話形式のコンテンツが提供されていた。これがすごく良くて、例えばコンテキストを考慮した推薦 (context-aware recommendation) について話してくれたのは、 Recommender Systems Handbook の編集者・Francesco Ricci先生だった！業界のトッププレイヤーたちから基礎が学べるなんて、いい時代に生まれたものだと思う。
推薦アルゴリズムの基本は、ユーザ・アイテム間の履歴（e.g., クリックした/してない、高評価/低評価）を以下のような行列のかたちで表現するところにある。なお、要素が取りうる値は0/1や実数値、具体的な5段階の評価値まで様々。
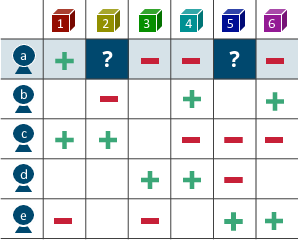
そして、僕らが解くべき問題は行列の未観測値を予測することであり、予測値を元に「この人はどんなアイテムを好みそうか」という傾向を見つけていく。
このコースでは最初に 非個人化推薦 (Non-Personalized Recommender) を扱う。具体的には、『最も人気のアイテムを常に推薦する』であったり、『行列の未観測値は、その行（列）の平均値で埋める』であったり、そんな頭の悪そうな手法。しかしこんな手法でも、データによっては高度なアルゴリズムよりも高い精度を叩き出すことがあるので侮れない。推薦システムを作りたいときはこういうナイーブなところから始めるのも悪くない。
次に扱うのは 個人化推薦 (Personalized Recommender) で、数式や機械学習を使った賢そうな手法の多くはこれに該当する。中でも特に重要な手法は、Amazonの「この商品を買った人はこちらの商品も〜」で有名な 協調フィルタリング (Collaborative Filtering) だろう。
協調フィルタリング
協調フィルタリングにはユーザ間類似度に基づく方法 (user-based) とアイテム間類似度に基づく方法 (item-based) の二種類がある。どちらも基本は同じで、行（列）のペアに対して計算した類似度に基づいて未観測値を予測して、予測値の高いアイテムから上位N件を推薦する。以下は5段階の評価値行列に対する協調フィルタリングのイメージ。"Item-Based Collaborative Filtering Recommendation Algorithms"の図1に倣って書いた。
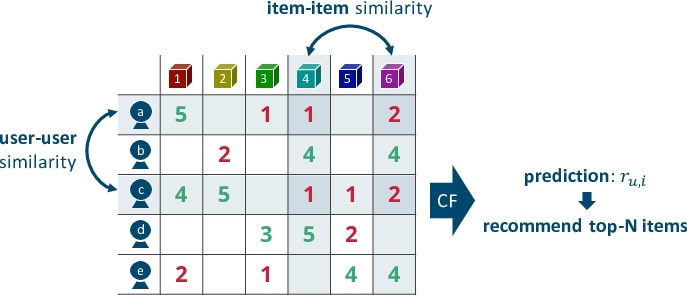
講義の中では「user-basedとitem-based、どちらが良いのか？」という問いにも答えていた。一般に、世の中のインターネットサービスは膨大なユーザを抱えており、各ユーザの趣味・嗜好は動的に変化する。ゆえに、ユーザ間類似度は計算が非効率で、かつ頻繁な再計算が必要となる。一方、アイテム数はユーザ数に比べると十分に少なく、それらの特徴はある程度静的だ。というわけで、user-basedよりもitem-basedのほうが現実的な選択と言える。
類似度についてはピアソン相関係数から始まり、正規化、コサイン類似度との関連について丁寧に解説されていた。おかげで、「協調フィルタリングの”気持ち”は分かったけど、どうやって実装すれば良いのか…」ということにはならない。以前読んだ『実践 機械学習』は、”気持ち”の解説に徹していて数学的な処理はブラックボックスのままだった。
次元削減（特異値分解、Matrix Factorization）
ひと通り協調フィルタリングを解説すると、講義では以下のような問題点が指摘される。
- ユーザ・アイテム間行列が巨大すぎて、すべてのユーザ（アイテム）ペアについて類似度計算を行うのは非現実的
- この行列は一般に疎（スパース；要素の多くが未観測値）なので、計算された類似度が有意義だとは言い難い
そこで「ユーザ・アイテム間の行列からできるだけ効率的に、より本質的なユーザの趣味・嗜好を抽出したい」というモチベーションから生まれた、協調フィルタリングの先にある推薦手法が 特異値分解 に基づくもの。
特異値分解は与えられた行列 $A$ を $U$, $\Sigma$, $V$ の3つに分解する手続きで、$A$がユーザ・アイテム間行列だとすれば、$U$はユーザに関する特徴が詰まった行列、$V$はアイテムに関する特徴が詰まった行列、$\Sigma$はそれらに与える重み、に相当する。
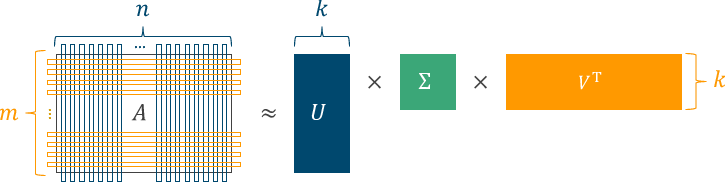
これらの積 $\hat{A} = U \Sigma V^{\mathrm{T}}$ は元の行列 $A$ の近似になっていて、$A$で未観測だった要素も$\hat{A}$ではなんらかの値が入っている。この値を予測値とみなして推薦をしましょう、というのが基本的なアイディア。
ちなみにPython + numpyならこんな感じ。
import numpy as np
import numpy.linalg as ln
# ユーザ5人、アイテム6つに対する行列（0は観測値）
A = np.array([[5, 0, 1, 1, 0, 2],
[0, 2, 0, 4, 0, 4],
[4, 5, 0, 1, 1, 2],
[0, 0, 3, 5, 2, 0],
[2, 0, 1, 0, 4, 4]])
U, s, V = ln.svd(A, full_matrices=False)
# どれくらいの粒度で近似するか
k = 2
A_ = np.dot(np.dot(U[:, :k], np.diag(s[:k])), V[:k, :])
# [[ 3.19741238 1.98064059 0.19763307 0.50430074 1.04148574 2.47123826]
# [ 1.20450954 1.18625722 1.50361641 3.5812116 1.61569345 2.37803076]
# [ 4.36792826 2.68465163 0.20157659 0.52659617 1.36419993 3.30665072]
# [-0.94009727 0.07701659 2.08296828 4.93223799 1.52652414 1.44132726]
# [ 2.67985286 1.80342544 0.63125085 1.52750202 1.27145836 2.54266834]]
ただしこの手法には重大な問題があって、未観測値をゼロで埋めている。5段階の評価値行列で0とは、すなわち「全く興味がない」に相当する。しかし本来、行列の未観測値には2種類の意味ある。
- 全く興味がないからスルーしていた
- そもそもユーザはそのアイテムの存在に気づいていなかった
どちらの意味で”未観測”なのかが判断できない以上、テキトーな値で補完して処理を行うのはナンセンスだ。というわけで Matrix Factorization へと話が進む。これも行列を分解する手続きの一種で、$R$という行列を$P$と$Q$に分解する。
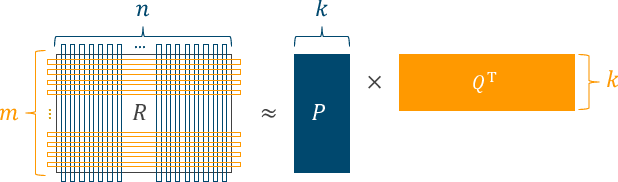
特異値分解と比較すると、$U$が$P$に相当して、$V$が$Q$に相当する。ただし、重み$\Sigma$は$P$, $Q$の内部に埋め込まれている、というイメージ。
Matrix Factorizationのキモは、逐次的なアルゴリズムよって観測した値のみを使って行列を分解するところにある。
推薦の文脈での初出はNetflix Prizeの最中に投稿されたSimon Funkのブログエントリで、これが学術論文でめちゃめちゃ引用されている！1ブログエントリから始まった手法は今や業界では定番中の定番な手法となり、その先にあるProbabilistic Matrix Factorization、Tensor Factorization、Factorization Machinesなど、すべてはここを土台に議論ができる。
本当はこの先にあるもっと機械学習っぽい手法がアツくて面白いのだけど、そこは推薦システムの本質ではない。すべての基礎はこのコースで扱う話題の範囲内にあるのだと思う。ヒューリスティクスや非個人化手法が勝ることも十分ありうるわけだし。その意味で、Matrix Factorizationの導入までで講義を終え、より具体的かつ発展的な手法はすべてインタビューパートに回したコース構成はお見事だったと思う。
また、最終回にはAdvanced topicsとして、cold-start問題（履歴が存在しない新規ユーザ・アイテムに対して推薦をするのが難しい問題）に関する議論や、実践的な視点でのインタビューがあった。
まとめ
協調フィルタリングが発明されてから、Netflix Prizeを経てMatrix Factorizationの登場に至るまでの経緯が整理されたとても良いコースだった。手法や事例が無数に存在する分野なので、書籍やサーベイ論文を読んでもこのあたりを順序立てて学ぶのは結構難しかったりする。
インターン先のメンターにオススメされて受講しはじめたものの、すでに知っていることも多かったので途中サボったりして修了までに半年くらいかかってしまった。とはいえ、終えてみると得られたものは結構多かったなぁという実感がある。何より、このコースのおかげで推薦システムについて書いた僕の修士論文のBackgroundの章はものすごく充実した（と思う）。
難点をあげるとすれば、課題がスプレッドシートの上で行うことを想定して作られていたことだろうか。これに素直に従うのは死ぬほど退屈なので、僕は与えられたデータをCSVに変換した後、Juliaで実装しながら課題を解いた。この実装たちはライブラリにまとめて公開したので、興味があればぜひ。記事にもまとめました。
余談だけど、ちょうど受講中に学生ボランティアとしてRecSys 2016に参加して、Konstan先生のユーモアや鋭い質問に間近で触れることができたのはマジ感動でした。さらに学生ボランティアの中にはKonstan先生のグループの学生もいて、その人は本会議に論文が採択されていて、ひょえ〜と思いつつ、とても高まった。
シェアする
カテゴリ
あわせて読みたい
- 2017-11-23
- 筋トレ、登山、昨今の推薦システムのトレンドなどについて話しました
- 2017-06-10
- Amazonの推薦システムの20年
- 2017-02-18
- "SLIM: Sparse Linear Methods for Top-N Recommender Systems"を読んだ
最終更新日: 2022-06-26
書いた人: たくち
Takuya Kitazawa（たくち）です。長野県出身、カナダ・バンクーバー在住のソフトウェアエンジニア。これまでB2B/B2Cの各領域で、Web技術・データサイエンス・機械学習のプロダクト化および顧客への導入支援・コンサルティング、そして関連分野の啓蒙活動に携わってきました。現在は主に北米（カナダ）、アジア（日本）、アフリカ（マラウイ）の個人および企業を対象にフリーランスとして活動中。詳しい経歴はレジュメ を参照ください。いろいろなまちを走って、時に自然と戯れながら、その時間その場所の「日常」を生きています。ご意見・ご感想およびお仕事のご相談は [email protected] まで。
近況 一杯のコーヒーを贈る免責事項
- Amazonのアソシエイトとして、当サイトは amazon.co.jp 上の適格販売により収入を得ています。
- 当サイトおよび関連するメディア上での発言はすべて私個人の見解であり、所属する（あるいは過去に所属した）組織のいかなる見解を代表するものでもありません。
- 当サイトのコンテンツ・情報につきまして、可能な限り正確な情報を掲載するよう努めておりますが、個人ブログという性質上、誤情報や客観性を欠いた意見が入り込んでいることもございます。いかなる場合でも、当サイトおよびリンク先に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。
- その他、記事の内容や掲載画像などに問題がございましたら、直接メールでご連絡ください。確認の後、対応させていただきます。