Given a sorted array arr, Array Bisection Algorithm (a.k.a. Bisection Method, Binary Search Method) enables us to find an insertion point i for a new element val such that arr[i-1] < val <= arr[i] (or, arr[i] < val <= arr[i+1]).
Problem
Consider we want to insert a number 10 to a sorted array [2, 4, 8, 16, 32]. Here, an insertion point should be i=3 as arr[2] < 10 <= arr[3].
A naive method is sequentially walking through the elements until we hit the condition:
def search(arr, val):
"""
>>> search([2, 4, 8, 16, 32], 10)
3
"""
if val < arr[0]:
return 0
for i in range(1, len(arr)):
if arr[i-1] < val and val <= arr[i]:
return i
return len(arr)
The time complexity of this approach is $O(N)$, and larger arrays take more time to complete the operation.
Intuition
As an optimized way to solve the problem, binary search finds out an insertion point in $O(\log N)$ time complexity.
The basic idea of the method is to repeatedly split arr into two chunks, first-half arr[:mid] and last-half arr[mid+1:] of the elements, until a dividing point mid reaches the target value val.
A GIF image below from penjee.com illustrates how it works in comparison with the naive method:
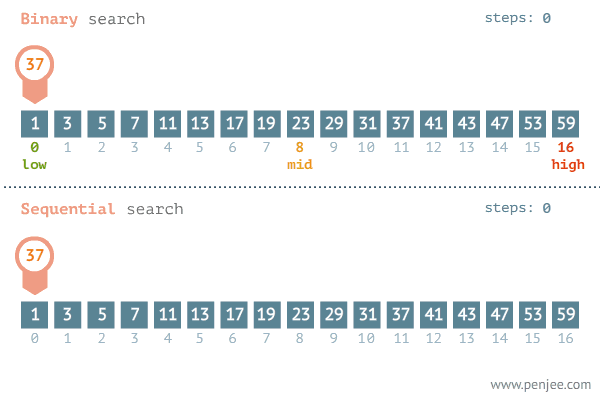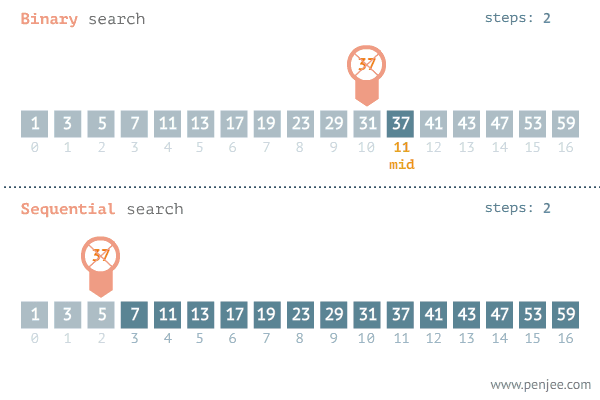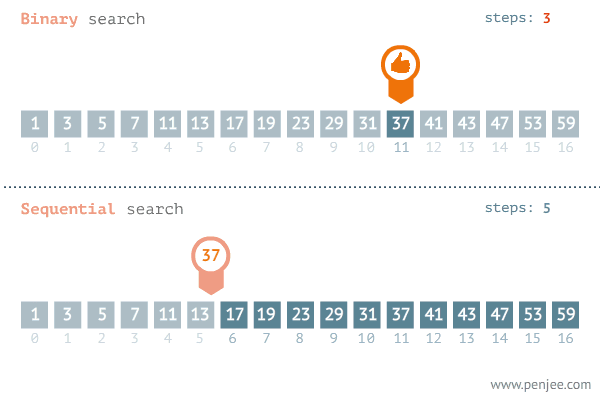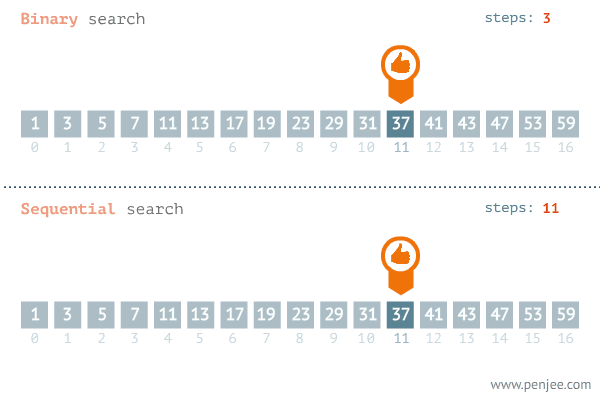
Implementation
Although Python implements the algorithm as a standard library bisect, let's try to implement it from scratch.
Starting from lo=0 and hi=len(arr)-1, what we have to do is to keep narrowing down a focused range while maintaining arr[lo] < val <= arr[hi].
def bisect(arr, val):
"""Bisection algorithm
Return an index of an ascending-ordered array `arr` where `val` can be inserted. A returned index `i` indicates a potential insertion point, and
`arr[i:]` must come after `val` once inserted.
>>> bisect([2, 4, 8, 16, 32], 1)
0
>>> bisect([2, 4, 8, 16, 32], 4)
1
>>> bisect([2, 4, 8, 16, 32], 3)
1
>>> bisect([2, 4, 8, 16, 32], 10)
3
>>> bisect([2, 4, 8, 16, 32], 64)
5
"""
if len(arr) == 0:
return 0
if val < arr[0]:
return 0
if arr[-1] < val:
return len(arr)
lo, hi = 0, len(arr) - 1
while lo < hi:
if val == arr[lo]:
return lo
elif val == arr[hi]:
return hi
mid = (lo + hi) // 2
if val == arr[mid]:
return mid
elif val < arr[mid]:
hi = mid
else:
lo = mid + 1
return lo
In the case of looking for a position where 10 fits in [2, 4, 8, 16, 32], the method updates lo and hi as follows.
First, all elements from head to tail are considered:
2 4 8 16 32
^ ^ ^
L M H
Next, the method realizes the first-half of the array elements is smaller than 10, and hence they are ignored so that the following process can focus only on the second half:
2 4 8 16 32
^ ^
M H
L
Finally, arr[2] < 10 <= arr[3] is confirmed, and 3 is returned as a potential insertion point:
2 4 8 16 32
^
H
M
L
Application
The bisection method can widely be applicable for searching a certain data point from historical records.
In real-world applications, it's safe to say that historical records arrive in the order of timestamp, and hence a target array is typically pre-ordered when we search something from there.
To give an example, assume you have a Tweet database for each user:
class User(object):
def __init__(self):
self.tweets = []
def tweet(self, datetime, text):
self.tweets.append((datetime, text))
The database sequentially stores a new tweet as soon as it's posted:
user = User()
user.tweet(20100101, 'Hello, world.')
# ...
user.tweet(20201201, 'I am hungry.')
user.tweet(20201231, 'Sleepy...')
user.tweet(202101015, 'Happy New Year!')
# ....
A question here could be "What was the last tweet in 2020?"
If we use bisect, an answer to the query can be easily and efficiently found by searching an insertion point for (20210101, ''):
def last_before(timestamp, arr):
"""
arr[i] := (timestamp, value)
"""
pos = bisect(arr, (timestamp, ''))
if pos == 0:
return ''
if pos == len(arr):
return arr[-1][1]
if arr[pos][0] == timestamp:
return arr[pos][1]
return arr[pos-1][1]
last_before(20210101, user.tweets) # => "Sleepy..."
Even if a target list is not pre-sorted, growing an array while maintaining its order is not hard when we leverage heap (sorted dictionary/queue, to be more precise). It only takes $O(\log N)$ for insertion.
The method itself is simple, but the efficient searching technique could accelerate a lot of real-life applications we can think of.
Share
Categories
See also
- 2021-04-04
- The Essence of Supply Chain Management
- 2017-01-21
- FluRS: A Python Library for Online Item Recommendation
- 2017-01-14
- Recommendation.jl: Building Recommender Systems in Julia
Last updated: 2022-09-02
Author: Takuya Kitazawa
Takuya Kitazawa is a freelance software developer, previously working at a Big Tech and Silicon Valley-based start-up company where he wore multiple hats as a full-stack software developer, machine learning engineer, data scientist, and product manager. At the intersection of technological and social aspects of data-driven applications, he is passionate about promoting the ethical use of information technologies through his mentoring, business consultation, and public engagement activities. See CV for more information, or contact at [email protected].
Support by donation Gift a cup of coffeeDisclaimer
- Opinions are my own and do not represent the views of organizations I am/was belonging to.
- I am doing my best to ensure the accuracy and fair use of the information. However, there might be some errors, outdated information, or biased subjective statements because the main purpose of this blog is to jot down my personal thoughts as soon as possible before conducting an extensive investigation. Visitors understand the limitations and rely on any information at their own risk.
- That said, if there is any issue with the content, please contact me so I can take the necessary action.