もしも推薦システムの精度と多様性が単一の指標で測れたら

2021-11-17

もしも推薦システムの精度と多様性が単一の指標で測れたら

RecSys 2021採択論文の中で気になっていた "Towards Unified Metrics for Accuracy and Diversity for Recommender Systems" を読んだ。

独特かつ曖昧な表記の数式が並ぶ「読んでいてイライラするタイプの論文」ではあったものの、推薦結果の Relevance（履歴に基づく類似度；古典的な“精度”に直結）と Novelty（ユーザにとっての推薦結果の新規性・多様性；セレンディピティに寄与）を相互に検討する際の論点、手法に求められる性質、実験のフレームワークのリファレンスとして有用な研究であるように思う。

一方、提案手法の筋の良さ、およびその実用性は疑わしい。定義の曖昧なパラメータを内在し、データに関して十分に事前知識のあるオフラインでの性能評価にユースケースを限定しているためだ。

いずれにせよ「精度の先にある、ユーザ本位で構築・評価される推薦システム」という業界のトレンドを反映した研究であることは確かであり、ざっくりと目を通しておいて損はないだろう。

After taking a quick look at the list of accepted papers, for me, one of the biggest trends in 2021 is user-centricity, which focuses on how to allow users to intervene in a recommendation process while minimizing the risk of biases and maximizing diversity & fairness of recommendations.

User-Centricity Matters: My Reading List from RecSys 2021

導入

Top-$k$アイテム推薦において、その結果の精度と多様性を同時に測るための新たな評価指標 $\alpha\beta$-$\mathrm{nDCG@}k$ を提案する。

議論の起点となるのは、 Item aspect という“カテゴリ”に相当する概念。あるアイテム $i$ は、1つ以上の Aspect $a_{\phi}$ に紐付く。そして“良い”推薦結果というものを定義するにあたって、マクロな視点で「カテゴリ単位で、推薦結果全体がユーザにもたらす満足度」の定量的表現を検討する、というのが本論文の仕事であると言える。

なお提案手法は、情報検索における検索結果の多様化に関する議論 "Search Result Diversification" を土台としている。

精度と多様性を兼ね備えた“良い”推薦結果とは？

ユーザの嗜好を過不足なくモデリングしつつ、アウトプットにはある程度の多様性を取り入れる—そのような「いいとこ取り」な推薦システムの構築を目指す場合、その良し悪しを定量的に評価するための指標は次の8つの性質を的確に捉えるべきである、と著者は言う。

Priority Inside Aspect: ある2つのアイテムの属するカテゴリ群が同一であれば、ユーザがより高評価を付けた（付けうる）アイテムがランキング上位で推薦される。
Deepness Inside Aspect: よりユーザの関心にマッチしているアイテムほど、ランキング上位にまとまって推薦されれる（必要以上に下位まで分散させない）。
Non Priority on Saturated Aspect: ユーザは、ある特定のカテゴリに属するアイテムを既に十分見せられた後で新たに2つのアイテムが提示された場合、（たとえ過去に低評価をつけていても）見飽きていない方のカテゴリと紐付くアイテムを好む。
Top Heaviness Threshold: ユーザは、興味にマッチするアイテムをランキング上位でピンポイントに見つけたい。興味があるからといって、ダラダラと似たような傾向のアイテムばかりが並ぶランキングを見たいわけではない。
Top Heaviness Threshold Complementary: ユーザに提示するアイテムの総数は多すぎないこと。ランク付けされた推薦結果を1位から最下位まですべて見るほど、彼ら・彼女らも暇ではない。
Aspect Relevance: ユーザはカテゴリ (Aspect) 単位で好みがあって、仮に2つのアイテムの両方が好きだったとしても、より好むカテゴリと紐付く方をより一層好む。
Prefer More Aspect Combination: ユーザは、ある2つのアイテムが等しく興味とマッチしている場合、これまでの推薦結果を振り返ってまだ十分に満足できていないカテゴリに属するアイテムをより一層好む。
Missing Over Non-Relevant: ユーザは、明らかに低評価をつける（自分は既にそれが嫌いであると知っている）アイテムよりは、全く見たことのない未知のアイテムを好む。

そして $\alpha\beta$-$\mathrm{nDCG@}k$ は上記すべての性質を定量的に評価することのできる指標である—すなわち性質を満たす推薦結果には高い値を、そうでない場合は低い値を返す—と。

いかにも都合よく並べられた仮定であるように思えるが、「精度の最大化だけを目的にスコアリング/ソートされたような、冗長で“つまらない”推薦結果は評価しない」という主張には共感する。

$\alpha\beta$-$\mathrm{nDCG@}k$ の気持ち

では『提案手法』である $\alpha\beta$-$\mathrm{nDCG@}k$ とは一体どのようなものなのか。

Top-$k$ランキング推薦における評価指標 Normalized Discounted Cumulative Gain (nDCG) とは、あるランク $1 \leq j \leq k$ における推薦の“質” (Gain) が $G_j$ で与えられるとき、$G_1, G_2, \cdots, G_j, \cdots, G_{k - 1}, G_k$ を総合的にみて次のように定量的な評価を与えるものである：

$\mathrm{nDCG@}k = \frac{\mathrm{DCG}_k}{\mathrm{IDCG}_k} = \frac{\sum_{j=1}^{k} G_j / \log_2(1+j)}{\mathrm{IDCG}_k}$

正規化係数 $\mathrm{IDCG}_k$ には近似解が用いられるわけだが [参考]、それはさておき、nDCG の言う "Gain" の定義は一意ではなくカスタマイズの余地が残されているという点がキモだ。

というわけで本論文の仕事はつまるところ、精度と多様性を同時に数値化してくれるような独自の $G_j$ を定義することにある。

先述の通り、僕らはユーザ $u$ の Aspect（カテゴリ）$a_{\phi}$ に対する興味・関心をモデリングすることによって、推薦結果をマクロなレベルで評価・最適化したい。というわけで具体的には、次に示すような「$1, 2, \cdots, k-1$ 番目までランク付けされた推薦アイテム列 $i_1, i_2, \cdots, i_{k-1}$ が与えられた時、$k$ 番目のアイテムとして $i$ がふさわしい確率」によってその推薦の“良さ”を判断する：

$1 - \prod_{\phi} \left( 1 - P\left(a_{\phi}\textrm{ への興味が満たされる} \mid u, i\right) \times P\left(i \textrm{ に } a_{\phi} \textrm{ であることを望む} \mid u, i_1, i_2, \cdots, i_{k-1} \right) \right)$

そして、この確率をTop-$k$推薦結果の "Gain" $G_k$ とみなして nDCG の定式化に当てはめてあげよう、という発想になる。

ここで $P\left(a_{\phi}\textrm{ への興味が満たされる} \mid u, i\right) = P(a_{\phi} \mid u,i)$ は「あるアイテム $i$ がユーザ $u$ の $a_{\phi}$ への興味を満たすのにどれだけ貢献しているか」を表しており、アイテムに対する直接的な評価値 $r_{u,i}$ を用いて次のように計算される：

$P(a_{\phi} \mid u,i )=\left\{ \begin{array}{ll} 0 & (i\textrm{ は }a_{\phi}\textrm{ に紐付かない}) \\ \alpha(u,i) & (i\textrm{ は }a_{\phi}\textrm{ に紐付くが }r_{u,i} \textrm{ は未観測}) \\ r_{u,i} / r_{\mathrm{max}} \times \beta(u) & (i\textrm{ が }a_{\phi}\textrm{ に紐付いて }r_{u,i}\textrm{ も分かっている}) \end{array} \right.$

$\alpha(u,i)$ はユーザ・アイテムペアから想定される適当な値であり、論文中では小さな定数としている。$r_{u,i}$ がわからない（＝事前知識が限られている）ためのナイーブな対応ではあるが、ユーザまたはアイテムの大域的なプロファイリングによって、より意味のある重み付けをすることは十分可能だろう。

$\beta(u)$ はユーザの評価の確度（どれだけ評価値が信用できるか；どれだけ評価がブレるか）を示すパラメータ。この値の最適化も、残念ながら著者は Future Work としている。

このように、Gain の計算に $\alpha$, $\beta$ という2つのパラメータが含まれる独自の nDCG であるから、提案手法を $\alpha\beta$-$\mathrm{nDCG@}k$ と呼んでいる。

先の確率の推定に至るまでの式変形は正直追いきれていない部分もあるため、ここでは著者プレゼンテーションのスライドを引用するに留めたい。

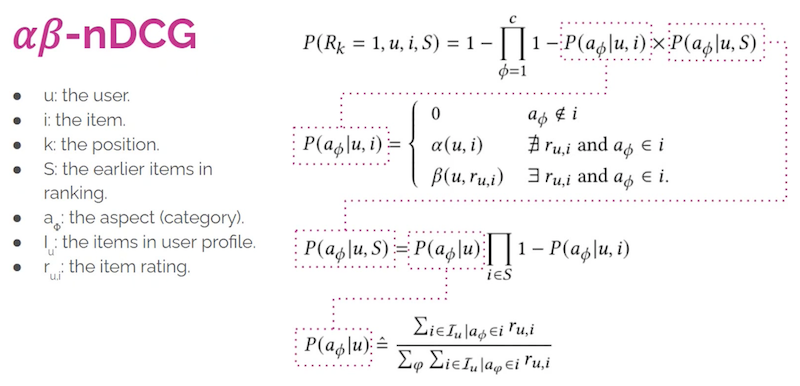
ab-ndcg

* "Towards Unified Metrics for Accuracy and Diversity for Recommender Systems"プレゼンテーション動画よりキャプチャ・引用。

いかにして「多様性」を測るか

「多様性」または「セレンディピティ」について議論することは難しい。過去に『Podcast "Data Skeptic" の推薦システム回が良すぎて3回聞いた』でも触れたように Serendipity = like + didn't expect であり、単純に奇をてらった推薦をしたらセレンディピティかというと、そういう話でもない。

先に挙げた性質その1 "Priority Inside Aspect"、その2 "Deepness Inside Aspect" が暗に語っているように、ユーザの好みを適切にモデリングした推薦結果であることは大前提だ。その上で、どこまで「好み」という直接的なフィードバックのみに忠実に従うべきか、という“程度”に関する問題なのだ。

提案された評価指標において、その“程度”をコントロールするために重要な役割を果たしているのが $\beta(u)$ の存在だ。これによりシステムは「ユーザが過去に高評価を付けたアイテムは全て良い」という短絡的な思考に陥らずに済む。

たとえば映画の5段階評価 $(r_{\mathrm{max}} = 5)$ で $i=$『鬼滅の刃』に★4をつけていた人 $u$ がいたとする。でも僕らは、この人の評価はジャンルに依らず結構ブレる（≒ジャンル問わず興味の幅が広い）と知っているので、信頼度は低めに見積もって $\beta(u)=0.2$ としよう。そのとき、映画『鬼滅の刃』に対する評価がこの人の $a_{\textrm{アニメ}}$ 欲を満たすのにどれだけ貢献しているのかといえば、それは微妙で $r_{u,i} / r_{\mathrm{max}} \times \beta(u) = 4/5 \times 0.2 = 0.16$ となる。逆に、評価に一貫性のある人ならば、たとえば $\beta(u)=0.9$ として $4/5\times 0.9 = 0.72$ であり、『鬼滅の刃』はそれだけでこの人のアニメ映画欲をかなり満たしてくれるといえる。

改めて Item aspect の定義に戻ると、ひとつのアイテムに対して複数の $a_{\phi}$ を取りうるので、『鬼滅の刃』がもたらす満足度は $P(a_{\textrm{アニメ}} \mid u,i )$ だけでなく $P(a_{\textrm{ファンタジー}} \mid u,i )$ や $P(a_{\textrm{フィクション}} \mid u,i )$ などによっても測られることに注意したい。

先の定式化における第一の確率 $P(a_{\phi} \mid u,i)$ は、この（正規化された）「重み付き評価値」をダイレクトに用いている。ゆえにこの確率は、アイテム評価値とカテゴリ別満足度を相互に見つつ、推薦結果の Relevance（精度）を測る役割を担っているといえる。

他方、第二の確率 $P\left(i \textrm{ に } a_{\phi} \textrm{ であることを望む} \mid u, i_1, i_2, \cdots, i_{k-1} \right)$（先のキャプチャ画像中の $P(a_{\phi}\mid u,S)$；$S$ はランク付けされたアイテム列 $i_1, i_2, \cdots, i_{k-1}$ ）では Novelty（新規性・多様性）を測っている。この確率の定式化には先の「満足度」とは反対の値が組み込まれていて、「$k-1$個の映画を見てもまだ満足できていないカテゴリ」を重視する：

$\prod_{\ell=1}^{k-1} \left( 1 - P(a_{\phi} \mid u, i_{\ell}) \right)$

先の例で言えば、$j=1$で既に『鬼滅の刃』をオススメしていたとしても、$P(a_{\textrm{アニメ}} \mid u,i_1 ) = 0.16$ と低い値を示しているのであれば、たとえ多様性を考慮したとしてもまずは引き続き $a_{\textrm{アニメ}}$ をオススメしたい、という話になる。したがって、たとえば同カテゴリに紐付く映画『呪術廻戦』は $j=2$ でも有望な候補となりうる。一方、仮に $\beta(u)=0.9$ で $P(a_{\textrm{アニメ}} \mid u,i_1 ) = 0.72$ であった場合、$j=2$ 以下、より早い段階で「もうアニメは十分です」というタイミングが訪れ、過度なアニメ映画の推薦は $\alpha\beta$-$\mathrm{nDCG@}k$ の低下に直結する。

雑感

というわけで、精度と多様性を統合した新しい推薦システム評価指標 $\alpha\beta$-$\mathrm{nDCG@}k$ を見た。冒頭にも述べたとおり、推薦結果の多様性という漠然とした問いに対して「“良い”ランキング推薦結果とはどのようなものか」を慎重に考え直すことによって立ち向かう、時代を反映した有意義な論文であったように思う。

しかし、そもそも精度と多様性を統合した単一の指標というものが本当に必要なのだろうか？

実験・評価用途であれば、精度指標 (Precision, Recall, nDCG) に加えて（比較的ナイーブな、独自の定義の下に）Novelty, Diversity も別途測定している研究は多数存在する。両者は常にトレードオフの関係にあるので、この場合は最終的には「手法Aは Precision が物凄く良いけれど、Diversity は手法Bに劣る」みたいな議論が展開される。これは $\alpha\beta$-$\mathrm{nDCG@}k$ として両者を畳み込んでしまった後ではおそらく困難な議論だ。

また、推薦アルゴリズムの学習に（損失関数として）用いるには明らかに議論が不足している。これは、Learning to Rank を始めとするランキング最適化手法の大衆化に伴い特に重要になっている視点だ。そもそも $\alpha$ や $\beta$ といったパラメータの値すら曖昧なのだ。なにをもって「最適な $\alpha\beta$-$\mathrm{nDCG@}k$」とするかは未だ自明ではない。

新しいパラメータを導入して作られた「わたしのかんがえたさいきょうの○○」は、ユースケースを限定してカリカリにチューニングされた状況下では良いのかもしれないが、そうでなければ議論をややこしくするだけの恐れもある。あなたにとっての「良い推薦システム」の定義はなんですか？まずはそんな根本的な問いについて今一度本気を出して考えてみることが、いまを生きる研究者・開発者には求められているのかもしれない。

カテゴリ

情報推薦

書いた人: たくち

Takuya Kitazawa（たくち）です。長野県出身、カナダ・バンクーバー在住のソフトウェアエンジニア。これまでB2B/B2Cの各領域で、Web技術・データサイエンス・機械学習のプロダクト化および顧客への導入支援・コンサルティング、そして関連分野の啓蒙活動に携わってきました。現在は主に北米（カナダ）、アジア（日本）、アフリカ（マラウイ）の個人および企業を対象にフリーランスとして活動中。詳しい経歴はレジュメを参照ください。いろいろなまちを走って、時に自然と戯れながら、その時間その場所の「日常」を生きています。ご意見・ご感想およびお仕事のご相談は [email protected] まで。

近況一杯のコーヒーを贈る

免責事項

Amazonのアソシエイトとして、当サイトは amazon.co.jp 上の適格販売により収入を得ています。
当サイトおよび関連するメディア上での発言はすべて私個人の見解であり、所属する（あるいは過去に所属した）組織のいかなる見解を代表するものでもありません。
当サイトのコンテンツ・情報につきまして、可能な限り正確な情報を掲載するよう努めておりますが、個人ブログという性質上、誤情報や客観性を欠いた意見が入り込んでいることもございます。いかなる場合でも、当サイトおよびリンク先に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。
その他、記事の内容や掲載画像などに問題がございましたら、直接メールでご連絡ください。確認の後、対応させていただきます。