不均衡データ (imbalanced data) からクラス分類を行うとき、マイナーなクラスに属するサンプルの oversampling や、メジャーなクラスに属するサンプルの undersampling (downsampling とも) が大切（cf.『不均衡データのクラス分類』）：

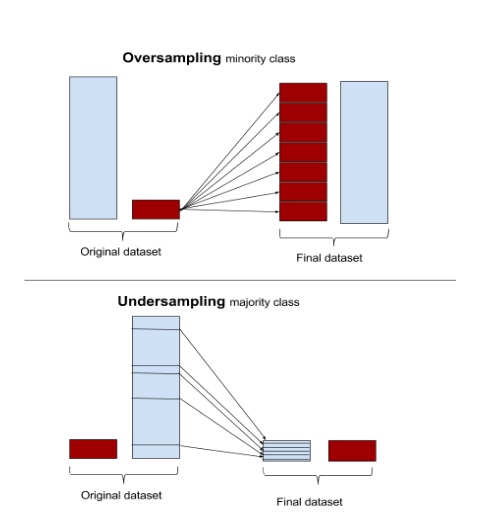
（▲ Tom Fawcett氏による記事 "Learning from imbalanced data" 中の5番目の図を引用）

このテクニックを使って学習した分類器による予測確率は、少し調整してから解釈したほうがいいらしい、という話。

Imbalanced data と Oversampling/Undersampling

たとえば2クラス分類をしたいとき、ラベル1のサンプル（正例）がわずか 0.01% しか存在せず、その他 99.99% のサンプルはラベル0（負例）、みたいな状況がある。

そこまで顕著ではないにせよ、現実のデータは正例/負例いずれかに大きく偏ったものであることが多い。具体的には、オンライン広告のクリック（正例） or 非クリック（負例）など。表示される広告を律儀に全部クリックする人などいないわけで、わずかな正例と大量の負例から「この人がクリックしてくれそうな広告」を予測、配信している。

正例 0.01%、負例 99.99% のときは、もはや機械学習なんかせず、常に「これは負例だ」と答える“分類器”を用意しても、評価段階では十分な精度が得られてしまうだろう。または、仮にそのサンプルで真面目に分類器を学習したとしても、正例はノイズ程度に扱われ、ほぼすべての入力に対して無条件に負例と予測する分類器になりかねない。

というわけで、imbalanced data のクラス分類を行うためには、oversampling または undersampling によってサンプル数を均等にしてあげて、フェアな条件で分類器を学習することが有効なのである。わずかな例外的サンプルに振り回されることがなくなるので、早く収束することも期待できる。

手法としては SMOTE (Synthetic Minority Oversampling Technique) などが有名だが、ここでは最も単純なランダムサンプリングだけを考える。メジャーなサンプルがマイナーなサンプルよりも $N$ 倍多いとき、

• Oversampling: マイナーなサンプルを $N$ 倍 (oversampling rate) に複製する
• Undersampling: メジャーなサンプルを $1/N$ 倍 (undersampling rate) に間引く

という操作をランダムに選んだサンプルを使って行う。

Undersampling時の予測確率の調整

引き続き2クラス分類を考える。

Facebookの広告クリック予測に関する論文を読むと、次のような記述がある：

• Practical Lessons from Predicting Clicks on Ads at Facebook

Negative downsampling can speed up training and improve model performance. Note that, if a model is trained in a data set with negative downsampling, it also calibrates the prediction in the downsampling space.

彼らのクリック予測モデルは決定木とロジスティック回帰を組み合わせたもの。その学習に際して、負例の undersampling (negative downsampling) を検討している¹。先の引用で言っているのは、undersampling rate $w$ で学習したモデルによる予測確率 $p$ は、最終的に：

$$\frac{p}{p + (1 - p) / w}$$

このように調整してから使うと良いですよ、という話。直感的には、間引いた分だけ負例の予測確率 $1 - p$ が押し下げられているので、“間引き率”に基づいて上方修正してあげましょう、という気持ちだろうか。

ちなみにこの式を真面目に導出することもできて、たとえば "When is undersampling effective in unbalanced classification tasks?" の2章なんかが参考になる²。

Imbalanced な元データ $(\mathcal{X}, \mathcal{Y})$ からメジャーなクラスを undersampling して学習データ $(X, Y)$ を得たとき³、元の不均衡サンプル $(x,y) \in (\mathcal{X}, \mathcal{Y})$ が学習データに含まれているか否かを表すバイナリ変数 $s$ を考える。すると、

• $p(s=1 \mid y=1)$
  • = 元データの正例が undersampling された学習データに含まれる確率
  • ~ 正例の undersampling rate
• $p(s=1 \mid y=0)$
  • = 元データの負例が undersampling された学習データに含まれる確率
  • ~ 負例の undersampling rate

ということになる。

そして、undersampling によって作ったデータで学習された分類器が出力する確率は、データが均衡であることを仮定するので $p(y \mid x, s=1)$ と書ける。一方で何も仮定しない、任意のサンプルに対する予測確率は $p(y \mid x)$ である。

ここで簡単のため、前者を $p_s = p(y=1 \mid x, s=1)$、後者を $p = p(y=1 \mid x)$ とおこう。つまり $p(y=0 \mid x) = 1 - p$ である。

さて、先の論文によると、ベイズの定理から両者の間には次のような関係があることがわかる：

$$p_s = \frac{\alpha \ p}{\alpha \ p + \beta \ (1-p)}$$

※ $\alpha = p(s=1 \mid y=1)$、$\beta = p(s=1 \mid y=0)$ とおいた。

$p_s \neq p$ であり、undersampling が予測確率それ自体にバイアスをかけているのだ。

通常 undersampling の対象となるのは正例/負例のうちメジャーな一方のみなので、たとえば負例を undersampling したなら、先の関係式は $\alpha = 1$ で：

$$p_s = \frac{p}{p + \beta \ (1-p)}$$

となる。

僕らは imbalanced data からいい感じの分類器を得るために undersampling をした。その結果、分類器は予測確率 $p_s$ を出力する。しかし本来、未知のデータはやっぱり imbalanced なのだから、真に知りたいのは $p$ である。というわけで、この式を変形して、$p_s$ から $p$ を求められるようにしよう：

$$p = \frac{\beta \ p_s}{\beta \ p_s - p_s + 1} = \frac{p_s}{p_s + (1 - p_s) / \beta}$$

おわかりいただけただろうか。負例の undersampling rate $w = \beta$ とすれば、Facebook論文の予測確率を調整する式になる。

なお、正例のほうが多かった場合はそっちを rate $\alpha$ で undersampling するので、$\beta = 1$ となり：

$$p = \frac{p_s / \alpha}{p_s / \alpha + (1-p_s)}$$

こんな感じで調整できる。

Oversamplingの場合

正例または負例の undersampling rate $0 \leq \alpha, \ \beta \leq 1$ を使って予測確率を調整する式：

$$p = \frac{p_s / \alpha}{p_s / \alpha + (1-p_s) / \beta}$$

が存在することが分かった。

Oversampling の場合は対照的に、底上げされてしまった予測確率の下方修正をすることになる。

つまり $\alpha, \beta$ が oversampling rate なら、$\alpha, \ \beta \geq 1$ なので、同じ調整式を使って $p_s / \alpha$ や $(1-p_s)/\beta$ でそのクラスの予測確率を“何倍に複製したか”に応じて小さめに調整することになる。

ただ、これは確率としての undersampling rate $p(s \mid y)$ の議論から外れてしまう。Oversampling の場合で先の調整式を導出している論文はまだ発見できていないけど、あるのかな。ちなみに、以下のページには同様の式が登場するので、直感的な解釈としては割とよくある考え方らしい：

• Adjusting for Oversampling
• Oversampling for Rare Event

まとめ

Oversampling/Undersampling によってマイナーなクラスも正しく分類できるようになる。しかし同時に、予測確率に若干バイアスがかかってしまう。

単に『予測確率の上位k件』が得たいのであればそれでも問題ないけど、予測値そのものを使いたい場合は、over-/under-sampling rate に応じて値を調整してあげる必要がありますよ、というお話でした。

¹. Imbalanced data であるか否かに依らず、そもそも彼らのデータは膨大すぎるので、学習コストを抑えるべく事前にある程度データを間引きたいというモチベーションがある。なので単にサンプル全体から学習データを uniform sampling をすることも検討されている。 ↩

². Facebook論文にはreferenceがないけど、この予測確率を調整する式はそんなに当たり前のモノなんだろうか…。 ↩

³. つまり $(X, Y) \subset (\mathcal{X}, \mathcal{Y})$ ↩

  シェアする

Tweet

  カテゴリ

機械学習

  あわせて読みたい

2017-12-01

『Java本格入門』メモ

2017-08-26

異常検知のための未来予測：オウム返し的手法からHolt-Winters Methodまで

2017-03-04

Area Under the ROC Curve (AUC) を実装する

  もっと見る

最終更新日: 2022-01-18

  書いた人: たくち

Takuya Kitazawa（たくち）です。長野県出身、カナダ・バンクーバー在住のソフトウェアエンジニア。これまでB2B/B2Cの各領域で、Web技術・データサイエンス・機械学習のプロダクト化および顧客への導入支援・コンサルティング、そして関連分野の啓蒙活動に携わってきました。現在は主に北米（カナダ）、アジア（日本）、アフリカ（マラウイ）の個人および企業を対象にフリーランスとして活動中。詳しい経歴はレジュメ を参照ください。いろいろなまちを走って、時に自然と戯れながら、その時間その場所の「日常」を生きています。ご意見・ご感想およびお仕事のご相談は [email protected] まで。

  近況   一杯のコーヒーを贈る

  免責事項

• Amazonのアソシエイトとして、当サイトは amazon.co.jp 上の適格販売により収入を得ています。
• 当サイトおよび関連するメディア上での発言はすべて私個人の見解であり、所属する（あるいは過去に所属した）組織のいかなる見解を代表するものでもありません。
• 当サイトのコンテンツ・情報につきまして、可能な限り正確な情報を掲載するよう努めておりますが、個人ブログという性質上、誤情報や客観性を欠いた意見が入り込んでいることもございます。いかなる場合でも、当サイトおよびリンク先に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。
• その他、記事の内容や掲載画像などに問題がございましたら、直接メールでご連絡ください。確認の後、対応させていただきます。